Answer:
4.6cm
Explanation:
A diagram showing the analysis from the question has been attached to this response. Kindly download it and view.
From the diagram,
=> We have three angles given
(i) the right angle, 90°
(ii) the angle opposite to side x, 50°
(iii) the angle opposite to side y, 40°
=> We also have one side given,
(i) the hypotenuse, of length 6cm
We can therefore apply the sine rule as follows;
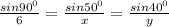 ---------------(i)
---------------(i)
Now to get the value of x, we'll equation the first and second terms of equation (i) as follows;
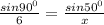 [cross multiply]
[cross multiply]


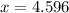 cm = 4.6cm [to the nearest tenth]
cm = 4.6cm [to the nearest tenth]
Therefore, the value of x is 4.6cm to the nearest tenth