Answer:
As per the properties of parallel lines and interior alternate angles postulate, we can prove that:
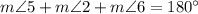
Explanation:
Given:
Line y || z
i.e. y is parallel to z.
To Prove:
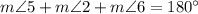
Solution:
It is given that the lines y and z are parallel to each other.
 are interior alternate angles because lines y and z are parallel and one line AC cuts them.
are interior alternate angles because lines y and z are parallel and one line AC cuts them.
So,
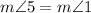 ..... (1)
..... (1)
Similarly,
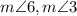 are interior alternate angles because lines y and z are parallel and one line AB cuts them.
are interior alternate angles because lines y and z are parallel and one line AB cuts them.
So,
 ...... (2)
...... (2)
Now, we know that the line y is a straight line and A is one point on it.
Sum of all the angles on one side of a line on a point is always equal to
 .
.
i.e.
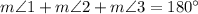
Using equations (1) and (2):
We can see that:
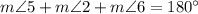
Hence proved.