Answer:
12.56
 is the error in area of circle.
is the error in area of circle.
Explanation:
Given that:
Radius of the circle, r = 10 cm
Error in measurement of radius,
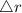 = 0.2 cm
= 0.2 cm
To find:
The error in area of circle = ?
Solution:
First of all, let us have a look at the percentage error in measurement of radius:
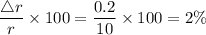
Now, we know that Area of a circle is given as:
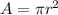

Area according to r = 10
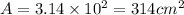
Now, error in area = 4% of 314

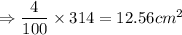
So, the answer is:
12.56
 is the error in area of circle.
is the error in area of circle.