Question

The radius of a circle is given as 10cm subject to an error of 0.2cm. the error in the area of the circle is?

​

Answer 1

12.56
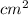`cm^2` is the error in area of circle.

Explanation:

Given that:

Radius of the circle, r = 10 cm

Error in measurement of radius,
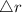`\triangle r` = 0.2 cm

To find:

The error in area of circle = ?

Solution:

First of all, let us have a look at the percentage error in measurement of radius:

`(\triangle r)/(r)* 100 = (0.2)/(10)* 100 = 2\%`

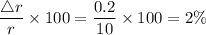
Now, we know that Area of a circle is given as:

`A = \pi r^2`

`\Rightarrow (\triangle A)/(A) * 100 = 2 * (\triangle r)/(r) * 100\\\Rightarrow (\triangle A)/(A) = 4\%`

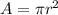
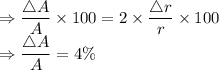
Area according to r = 10

`A = 3.14* 10^2 = 314 cm^2`

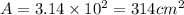
Now, error in area = 4% of 314
`cm^2`

`\Rightarrow (4)/(100) * 314 = 12.56 cm^2`

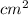
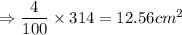
So, the answer is:

12.56
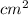`cm^2` is the error in area of circle.