Question

A 30.0-g object moving to the right at 19.5 cm/s overtakes and collides elastically with a 13.0-g object moving in the same direction at 15.0 cm/s. Find the velocity of each object after the collision. (Take the positive direction to be to the right. Indicate the direction with the sign of your answer.) 30.0-g object Incorrect: Your answer is incorrect. seenKey 16.8 Your response differs significantly from the correct answer. Rework your solution from the beginning and check each step carefully. cm/s 13.0-g object

Answer 1

`V(30g)=1.4(cm)/(s) \\V(13g)=5.9(cm)/(s)`

Step-by-step explanation:

So my calculations may be off (the final step is plugging in a bunch of things and getting a value, which creates room for error [and they honestly seem too small]) but I'm confident that the process is correct. I'll upload my work shortly but here is the method:

1. Use the Principle of Conservation of Momentum (PCoM) to set up a statement between the momentum of each object before and after the collision. It should be [before]=[after] because the collision is said to be elastic.
2. Do the same thing using the Principle of Conservation of Energy (PCoE). Note that you can start with either one, the problem can't really be done without both anyways.
3. You can chose to either divide the PCoM expression by the PCoE expression or do a series of substitutions. If you do the sub., you'll find that it's the same thing as just dividing them outright. (This is a little time saving trick I picked up from one of my Physics professors, I definitely didn't come up with it on my own.)
4. After that, you should be able to reduce the expressions into something with only the two initial velocities and the two final velocities. Note that in order to reduce, you'll need to use the "difference of squares" relationship in the PCoE expression. Choose either one of the final velocities to solve for first via substitution. In my example, I chose to solve for the 30g mass's final velocty first by subbing out the 13g mass's final velocity. (If you do it the other way around, your work might look different from mine at the end but it should give the same answer either way.)
5. After substituting, you should have an expression where the final velocity equals some combination of the masses and initial velocities of both objects (it's not a "nice" looking equation).
6. With one final velocity found, you can plug it into the expression you found in step 4. to find the other mass's final velocity.

And with that, you've got it! This whole process is kinda long and involved so I would try practicing it a lot before any tests/quizzes so it doesn't eat up your time.

Edit: In my work I made u to be the initial velocities and v to be the final velocities because it was easier to keep track of

Answer 2

The final velocity of the 30 g object is 16.8 cm/s

The final velocity of the 13 g object is 21.3 cm/s

Step-by-step explanation:

Let's study the elastic collision with conservation of linear momentum, assigning object 1 to the 30 g object, and object 2 to the 13 gr object:

`p_(1\,i)+p_(2\,i)=p_(1\.f)+p_(2\,f)\\(30)\,(19.5)+(13)\,(15) = (30)\,v_(1\,f) +(13)\,v_(2\,f)\\780 = (30)\,v_(1\,f) +(13)\,v_(2\,f)`

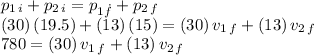
so we can write one of the unknowns in terms of the other one:

`v_(1\,f)=(780-13\,v_(2\,f))/30`

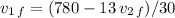
Now we analyze the equation for conservation of kinetic energy that verifies in elastic collisions:

`(30)/(2) (19.5)^2+(13)/(2) \,(15)^2=(30)/(2) (v_(1\,f))^2+(13)/(2) \,(v_(2\,f))^2\\7166.25=15\, (v_(1\,f))^2+6.5\,(v_(2\,f))^2`

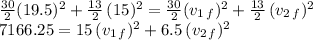
now we can write this quadratic equation replacing
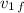`v_(1\,f)` with its expression in terms of
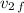`v_(2\,f)` and solve it (with the help of a graphing calculator is simpler by looking for the roots).

We get two answers for
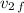`v_(2\,f)` : one 15 cm/s, and the other one 21.28 cm/s.

We select the 21.28 cm/s answer since otherwise, the situation is the same as the initial one at which the second object was moving at 15 cm/s.

This velocity can be rounded to one decimal to: 21.3 cm/s

Given the value 21,28 for
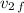`v_(2\,f)` , then:

`v_(1\,f)=(780-13\,v_(2\,f))/30\\v_(1\,f)=(780-13\,(21.28))/30=16.78 \,\,cm/s`

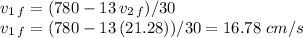
which can be rounded to 16.8 cm/s