Answer:
The mean and standard deviation of the number of cars recovered after being stolen is 522 and 8.24 respectively.
Explanation:
We are given that according to insurance records, a car with a certain protection system will be recovered 87% of the time.
Also, 600 stolen cars are randomly selected.
Let X = Number of cars recovered after being stolen
The above situation can be represented through binomial distribution;
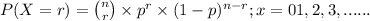
where, n = number of trials = 600 cars
r = number of success
p = probability of success which in our question is the probability
that car with a certain protection system will be recovered,
i.e. p = 87%.
So, X ~ Binom(n = 600, p = 0.87)
Now, the mean of X, E(X) =
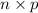
=
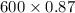 = 522
= 522
Also, the standard deviation of X, S.D.(X) =
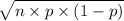
=
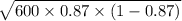
= 8.24