Answer:
The probability of the combination {H, T and H} is 0.125.
Explanation:
The sample space of flipping a quarter is:
S = {H and T}
The probability of both outcomes is same, i.e. P (H) = P (T) = 0.50.
It is provided that three quarters are flipped one at a time.
The outcomes of all the three quarters are independent of each other.
Compute the probability of the combination {H, T and H} as follows:
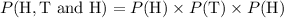
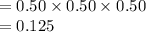
Thus, the probability of the combination {H, T and H} is 0.125.