Answer:
The answer is given below
Step-by-step explanation:
The question is not complete. Given that:
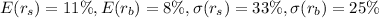 , ρ = 0.1560
, ρ = 0.1560
From the covariance matrix, Cov (B, S) =
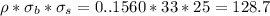
The minimum-variance portfolio is gotten using the formula:
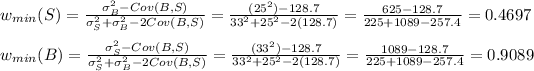
the expected return for the minimum-variance portfolio is:
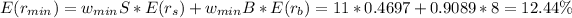
the standard deviation for the minimum-variance portfolio is:
![\sigma_(min)=[w_S^2\sigma_s^2+w_B^2\sigma_B^2+2w_Bw_SCov(B,S)]^(1)/(2) =[0.4687^2*33^2+0.9089^2*25^2+2*0.9089*0.4687*128.7]^(1)/(2)=29.41\%](https://img.qammunity.org/2021/formulas/business/college/c4535nlpm7ee71v3l4cc8t5rpg6ot77yuk.png)