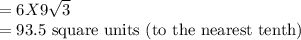Answer:
93.5 square units
Explanation:
Diameter of the Circle = 12 Units
Therefore:
Radius of the Circle = 12/2 =6 Units
Since the hexagon is regular, it consists of 6 equilateral triangles of side length 6 units.
Area of the Hexagon = 6 X Area of one equilateral triangle
Area of an equilateral triangle of side length s =
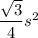
Side Length, s=6 Units
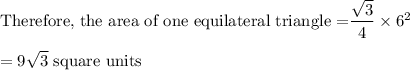
Area of the Hexagon