Answer:
Option (1). 17
Explanation:
Length of a segment having coordinates (x₁, y₁) and (x₂, y₂) is given by the formula,
d =
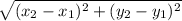
Coordinates of points A and C are (4, 3) and (19, 11).
To get the length of segment AC we will substitute the coordinates in the formula,
AC =
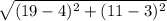
=

=

=
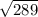
= 17
Therefore, length of segment AC = 17 units.
Option (1) will be the answer.