Question

An ideal reheat Rankine cycle with water as the working fluid operates the boiler at 15,000 kPa, the reheater at 2000 kPa, and the condenser at 100 kPa. The temperature is 4508C at the entrance of the high-pressure and lowpressure turbines. The mass flow rate through the cycle is 1.74 kg/s. Determine the power used by pumps, the power produced by the cycle, the rate of heat transfer in the reheater, and the thermal efficiency of this system

Answer 1

See the explanation below.

Step-by-step explanation:

First find the enthalpies h₁, h₂, h₃, h₄, h₅, and h₆.

Find h₁:

Using Saturated Water Table and given pressure p₁ = 100 kPa

h₁ = 417.5 kJ/kg

Find h₂:

In order to find h₂, add the
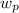`w_(p)` to h₁, where
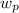`w_(p)` is the work done by pump and h₁ is the enthalpy computed above h₁ = 417.5 kJ/kg.

But first we need to compute
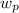`w_(p)` To computer

Pressures:

p₁ = 100 kPa

p₂ = 15,000 kPa

and

Using saturated water pressure table, the volume of water
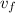`v_(f)` = 1.0432

Dividing 1.0432/1000 gives us:

Volume of water = v₁ = 0.001043 m³/kg

Compute the value of h₂:

h₂ = h₁ + v₁ (p₂ - p₁)

= 417.5 kJ/kg + 0.001043 m³/kg ( 15,000 kPa - 100 kPa)

= 417.5 + 0.001043 (14900)

= 417.5 + 15.5407

= 433.04 kJ/kg

Find h₃

Using steam table:

At pressure p₃ = 15000 kPa

and Temperature = T₃ = 450°C

Then h₃ = 3159 kJ/kg

The entropy s₃ = 6.14 kJ/ kg K

Find h₄

Since entropy s₃ is equal to s₄ So

s₄ = 6.14 kJ/kgK

To compute h₄

s₄ =
`s_(f)` +
`x_(4) s_(fg)`

`x_(4) = s_(4) -s_(f) /s_(fg)`

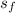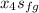
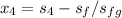
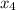`x_(4)` = 6.14 - 2.45 / 3.89

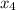`x_(4)` = 0.9497

The enthalpy h₄:

h₄ =
`h_(f) +x_(4) h_(fg)`

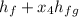
= 908.4 + 0.9497(1889.8)

= 908.4 + 1794.7430

= 2703 kJ/kg

This can simply be computed using the software for steam tables online. Just use the entropy s₃ = 6.14 kJ/ kg K and pressure p₄ = 2000 kPa

Find h₅

Using steam table:

At pressure p₅ = 2000 kPa

and Temperature = T₅ = 450°C

Then h₅ = 3358 kJ/kg

Find h₆:

Since the entropy s₅ = 7.286 kJ/kgK is equal s₆ to So

s₆ = 7.286 kJ/kgK = 7.29 kJ/kgK

To compute h₆

s₆ =
`s_(f)` +
`x_(6) s_(fg)`

`x_(6) = s_(6) -s_(f) /s_(fg)`

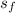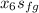
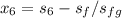
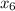`x_(6)` = 7.29 - 1.3028 / 6.0562

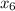`x_(6)` = 0.988

The enthalpy h₆:

h₆ =
`h_(f) +x_(6) h_(fg)`

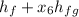
= 417.51 + 0.988 (2257.5)

= 417.51 + 2230.41

h₆ = 2648 kJ/kg

This can simply be computed using the software for steam tables online. Just use the entropy s₅ = 7.286 kJ/kgK and pressure p₅ = 2000 kPa

Compute power used by pump:

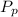`P_(p)` is found by using:

mass flow rate = m = 1.74 kg/s

Volume of water = v₁ = 0.001043 m³/kg

p₁ = 100 kPa

p₂ = 15,000 kPa

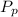`P_(p)` = ( m ) ( v₁ ) ( p₂ - p₁ )

= (1.74 kg/s) (0.001043 m³/kg) (15,000 kPa - 100 kPa)

= (1.74 kg/s) (0.001043 m³/kg) (14900)

= 27.04

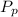`P_(p)` = 27 kW

Compute heat added
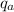`q_(a)` and heat rejected
`q_(r)` from boiler using computed enthalpies:

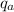`q_(a)` = ( h₃ - h₂ ) + ( h₅ - h₄ )

= ( 3159 kJ/kg - 433.04 kJ/kg ) + ( 3358 kJ/kg - 2703 kJ/kg )

= 2726 + 655

= 3381 kJ/kg

`q_(r)` = h₆ - h₁

= 2648 kJ/kg - 417.5 kJ/kg

= 2232 kJ/kg

Compute net work

W
`_(net)` =
`q_(a)` -
`q_(r)`

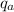= 3381 kJ/kg - 2232 kJ/kg

= 1150 kJ/kg

Compute power produced by the cycle

mass flow rate = m = 1.74 kg/s

W
`_(net)` = 1150 kJ/kg

P = m * W
`_(net)`

= 1.74 kg/s * 1150 kJ/kg

= 2001 kW

Compute rate of heat transfer in the reheater

Q = m * ( h₅ - h₄ )

= 1.74 kg/s * 655

= 1140 kW

Compute Thermal efficiency of this system

μ
`_(t)` = 1 -
`q_(r)` /
`q_(a)`

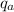
= 1 - 2232 kJ/kg / 3381 kJ/kg

= 1 - 0.6601

= 0.34

= 34%