Question

Water at 310 K and a flow rate of 4 kg/s enters an alumina tube (k=177Wm K1) with an inner diameter of 0.20 m and a wall thickness of 0.02 m. Air at a temperature of 390 K flows over the tube, heating it. The convection coefficients of for the water and air are 150 and 30 W m2 K-1, respectively.

Answer 1

Please find the attached graph of temperature as a function of tube length

Step-by-step explanation:

The given information are;

The temperature of the air = 310 K

The mass flow rate = 4 kg/s

k = 177 WmK1

The inner diameter of the tube = 0.20 m

The tube wall thickness = 0.02 m

The convection coefficients of the water = 150 W·m²/k

The convection coefficients of the water = 30 W·m²/k

The area of the tube = π×0.2^2/4 = 0.03142 m²

The density = 1000 kg.m³

The mass flow rate = 4 kg/s

`U_m = (\dot m)/(\rho \cdot A_c) = (4)/( 1000 * 0.03142) = 0.127 \ m/s`

`Re_(D) = (\rho * u_m * D)/(\mu) = (1000 \ kg/m^3 * 0.127 \ m/s * 0.2 \ m)/(8.01 * 10^(-4)\ N \cdot S/m^2) = 31,791.25`

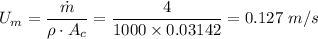
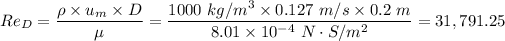
The Reynolds number is > 2300 for pipe therefore, we have turbulent flow, and the entry length is estimated at 10 pipe diameters

The Nusselt number, Nu = h*D/k = 0.023*31791.25^(0.8)*4.32^(0.4) = 165.11

The total resistance =
`R_(tot)=R_(conv, i) + R_(conv, i) + R_(tube)`

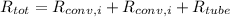
`R_(conv, i) + R_(conv, i)` = (1/150*(1/(0.2)) + 1/30*(1/(0.22)))/π = 0.059 K/W

Resistance of tube,
`R_(tube) = (ln(r_2/r_1)/(2\cdot \pi \cdot k) = (ln(0.12/0.1))/(2*\pi * 177) = 1.64 * 10^(-4) \ K/W`

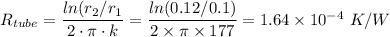
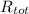`R_(tot)` = 0.059 + 1.64 × 10⁻⁴ = 0.059 K/W

The heat transfer
`\dot Q` =
`(t_A - t_B)/(R_(tot))`

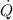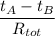
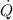`\dot Q` = (390 - 310)/0.059 = 1355.99 W ≈ 1356 W

Given that the water velocity = 0.127 m/s, we have;

Time to make one meter = 1/0.127 = 7.874 seconds

Mass of water that will have flowed in 7.874 seconds = 4×7.874 = 31.496 kg

The heat transferred in 7.874 seconds = 1356 × 7.874 = 10677.144 J

The specific heat capacity of water = 4,200 J/(kg·°C)

Therefore for one meter, we have;

10677.144 = 4,200 ×31.496 × (
`t_B` - 310)

(
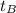`t_B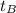` - 310) = 10677.144 /(4,200 *31.496) =

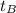`t_B` =0.0807 + 310 = 310.0807 K

At two meters, we have;

2*10677.144 = 2*4,200 *31.496 × (
`t_B` - 310)

(
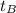`t_B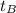` - 310.0807 ) = 2*10677.144 /( 2*4,200 *31.496 )

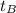`t_B` =0.0807 + 310.0807 = 310.1614

At three meters, we have

0.0807 + 310.0807 = 310.1614

The other values are;

m, T

1, 310.0807143

2, 310.1614286

3, 310.2421429

4, 310.3228571

5, 310.4035714

6, 310.4842857

7, 310.565

8, 310.6457143

Which gives the attached graph