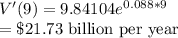Answer:
(a)In 2018, V(t)=$207.05 billion
In 2020, V(t)=$246.90 billion
(b)The export growth rate in 2018 is $18.22 billion per year
The export growth rate in 2020is $21.73 billion per year
Step-by-step explanation:
The value of exports, t years after 2011 can be approximated by:
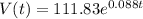
(a)We want to estimate the value of the country's travel exports in 2018 and 2020.
Now, 2018-2011=7 years
Therefore, in 2018
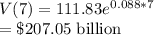
Now, 2020-2011=9 years
Similarly, in 2020
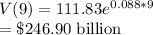
(b)Growth rate
If
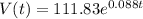 , then:
, then:
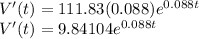
Growth rate in 2018 (at t=7)
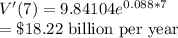
Growth rate in 2020 (at t=9)