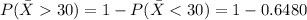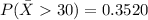Answer:
1
The probability is
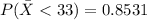
2
The probability is
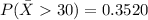
Explanation:
From the question we are told that
The population mean is
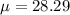
The standard deviation is
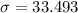
The sample size is

Generally the standard error for the sample mean
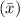 is mathematically evaluated as
is mathematically evaluated as
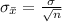
substituting values
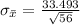
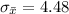
Apply central limit theorem[CLT] we have that
![P(\= X < 33) = [z < (33 - \mu )/(\sigma_(\= x)) ]](https://img.qammunity.org/2021/formulas/mathematics/college/5f02zln4gq6hg8qb3z77xai3l6d9qd0qw6.png)
substituting values
![P(\= X < 33) = [z < (33 - 28.29 )/(4.48) ]](https://img.qammunity.org/2021/formulas/mathematics/college/avmhqvlit02cd8gbcdjwazjx6wth01040h.png)
![P(\= X < 33) = [z < 1.05 ]](https://img.qammunity.org/2021/formulas/mathematics/college/lk971vclc2vn3rast4ufqrqwcnwtrp7b39.png)
From the z-table we have that
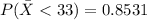
For the second question
Apply central limit theorem[CLT] we have that
![P(\= X > 30 ) = [z > (30 - \mu )/(\sigma_(\= x)) ]](https://img.qammunity.org/2021/formulas/mathematics/college/zir20njncl90cyx2s6cy7c26gqylqs2kb0.png)
substituting values
![P(\= X < 33) = [z > (30 - 28.29 )/(4.48) ]](https://img.qammunity.org/2021/formulas/mathematics/college/qhg2uo2wkssf9nrsqf4rnvg0v2pbt6eku8.png)
From the z-table we have that
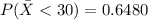
Thus