Answer:
The total number of maxima produced is
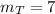 maxima
maxima
Step-by-step explanation:
From the question we are told that
The number of lines per cm is

The wavelength of the light is
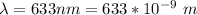
Now the distance between the lines is mathematically evaluated as
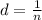
substituting values
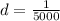
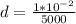 N/B - this statement convert it from cm to m
N/B - this statement convert it from cm to m
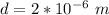
Generally the condition for diffraction i mathematically represented as
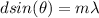
at maximum
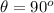
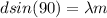
here m is the number of maxima
Thus making m the subject we have
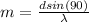
So

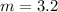
=> m =3
Now the total number of maxima would include the bright fringe(3) and dark fringe (3) plus the central maxima (1)
Thus

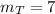 maxima
maxima