Question

A grating having 5000 lines/cm is used with light of wavelength 633 nm. How many total maxima (count central maxima plus all those on either side of the central maxima) are produced

Answer 1

The total number of maxima produced is
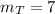`m_T = 7` maxima

Step-by-step explanation:

From the question we are told that

The number of lines per cm is
`n = 5000 \ lines/cm`

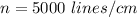
The wavelength of the light is
`\lambda = 633 nm = 633 *10^(-9) \ m`

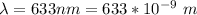
Now the distance between the lines is mathematically evaluated as

`d = (1)/(n)`

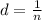
substituting values

`d = (1)/(5000)`

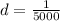
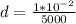`d = (1 *10^(-2))/(5000)` N/B - this statement convert it from cm to m

`d = 2 *10^( -6) \ m`

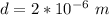
Generally the condition for diffraction i mathematically represented as

`dsin(\theta ) = m \lambda`

at maximum
`\theta = 90 ^o`

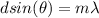
`d sin (90) = \lambda m`

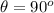
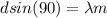
here m is the number of maxima

Thus making m the subject we have

`m = (d sin (90))/( \lambda )`

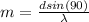
So
`m = (2*10^(-6) sin (90))/( 633 *10^(-9))`

`m = 3.2`

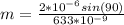
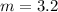
=> m =3

Now the total number of maxima would include the bright fringe(3) and dark fringe (3) plus the central maxima (1)

Thus

`m_T = 3 + 3 +1`

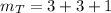
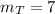`m_T = 7` maxima