Question

The paint used to make lines on roads must reflect enough light to be clearly visible at night. Let mu denote the true average reflectometer reading for a new type of paint under consideration. A test of

H0:μ=20 versus Ha:μ is greater than 20 will be based on a random sample of size n from a normal population distribution. What conclusion is appropriate in each of the following situations? (Round your P-values to three decimal places.)
a. n = 17, t = 3.1, α=0.05
State the conclusion in the problem context.
A. Do not reject the null hypothesis. There is not sufficient evidence to conclude that the new paint has a reflectometer reading higher than 20.
B. Reject the null hypothesis. There is not sufficient evidence to conclude that the new paint has a reflectometer reading higher than 20.
C. Do not reject the null hypothesis. There is sufficient evidence to conclude that the new paint has a reflectometer reading higher than 20.
D. Reject the null hypothesis. There is sufficient evidence to conclude that the new paint has a reflectometer reading higher than 20.
b. n = 10, t = 1.8, α=0.01
State the conclusion in the problem context.
A. Do not reject the null hypothesis. There is sufficient evidence to conclude that the new paint has a reflectometer reading higher than 20.
B. Reject the null hypothesis. There is not sufficient evidence to conclude that the new paint has a reflectometer reading higher than 20.
C. Do not reject the null hypothesis. There is not sufficient evidence to conclude that the new paint has a reflectometer reading higher than 20.
D. Reject the null hypothesis. There is sufficient evidence to conclude that the new paint has a reflectometer reading higher than 20.
c. n = 24, t = -0.4, p-value =

Answer 1

a) D. Reject the null hypothesis. There is sufficient evidence to conclude that the new paint has a reflectometer reading higher than 20.

b) C. Do not reject the null hypothesis. There is not sufficient evidence to conclude that the new paint has a reflectometer reading higher than 20.

Explanation:

a) We have a hypothesis test with the following hypothesis:

`H_0: \mu=20\\\\H_a:\mu> 20`

The significance level is 0.05 for this right-tailed test.

The sample size is n=17.

This means we have 16 degrees of freedom.

`df=n-1=17-1=16`

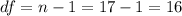
The test statistic has already been calculated and has a value of t=3.1.

This test is a right-tailed test, with 16 degrees of freedom and t=3.1, so the P-value for this test is calculated as (using a t-table):

`\text{P-value}=P(t>3.1)=0.0034`

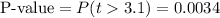
As the P-value (0.0034) is smaller than the significance level (0.05), the effect is significant.

The null hypothesis is rejected.

At a significance level of 0.05, there is enough evidence to support the claim that the new paint has a reflectometer reading higher than 20.

b. The hypothesis are the same as point a:

`H_0: \mu=20\\\\H_a:\mu> 20`

The degrees of freedom for this sample size are:

`df=n-1=10-1=9`

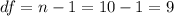
The significance level is 0.01.

The test statistic has already been calculated and has a value of t=1.8.

This test is a right-tailed test, with 9 degrees of freedom and t=1.8, so the P-value for this test is calculated as (using a t-table):

`\text{P-value}=P(t>1.8)=0.0527`

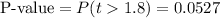
As the P-value (0.0527) is bigger than the significance level (0.01), the effect is not significant.

The null hypothesis failed to be rejected.

At a significance level of 0.01, there is not enough evidence to support the claim that the new paint has a reflectometer reading higher than 20.