Question

Air enters the first compressor stage of a cold-air standard Brayton cycle with regeneration and intercooling at 100 kPa, 300 K, with a mass flow rate of 6 kg/s. The overall compressor pressure ratio is 10, and the pressure ratios are the same across each compressor stage. The temperature at the inlet to the second compressor stage is 300 K. The turbine inlet temperature is 1400 K. The compressor stages and turbine each have isentropic efficiencies of 80% and the regenerator effectiveness is 80%. For k = 1.4, calculate:

a. the thermal efficiency of the cycle
b. the back work ratio
c. the net power developed, in kW
d. the rates of exergy destruction in each compressor stage and the turbine stage as well as the regenerator, in kW, for T 0 = 300 K.

Answer 1

a.
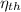`\eta _(th)` = 77.65%

b. bwr = 6.5%

c. 3538.986 kW

d. -163.169 kJ

Step-by-step explanation:

a. The given property are;

P₂/P₁ = 10, P₂ = 10 * 100 kPa = 1000 kPa

p₄/p₁ = 10

P₂/P₁ = p₄/p₃ = √10

p₂ = 100·√10

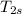`T_(2s)` = T₁×(√10)^(0.4/1.4) = 300 × (√10)^(0.4/1.4) = 416.85 K

T₂ = T₁ + (
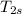`T_(2s)` - T₁)/
`\eta _c` = 300 + (416.85 - 300)/0.8 = 446.0625 K

p₄ = 10×p₁ = 10×100 = 1000 kPa

p₄/p₃ = √10 =

p₃ = 100·√10

T₃ = 300 K

T₃/
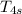`T_(4s)` = (P₂/P₁)^((k - 1)/k) = (√10)^(0.4/1.4)

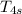`T_(4s)` = T₃/((√10)^(0.4/1.4) ) = 300/((√10)^(0.4/1.4)) = 215.905 K

T₄ = T₃ + (
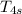`T_(4s)` - T₃)/
`\eta _c` = 300 + (215.905- 300)/0.8 = 194.881 K

The efficiency = 1 - (T₄ - T₁)/(T₃ - T₂) = 1 - (194.881 -300)/(300 -446.0625 ) = 0.28

T₄ = 446.0625 K

T₆ = 1400 K

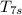`T_(7s)`/T₆ = (1/√10)^(0.4/1.4)

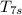`T_(7s)` = 1400×(1/√10)^(0.4/1.4) = 1007.6 K

T₇ = T₆ -
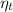`\eta _t`(T₆ -
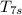`T_(7s)`) = 1400 - 0.8*(1400 - 1007.6) = 1086.08 K

T₈ = 1400 K

T₉ = 1086.08 K

T₅ = T₄ +
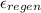`\epsilon _(regen)`(T₉ - T₄) = 446.0625 +0.8*(1086.08 - 446.0625) = 958.0765 K

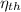`\eta _(th)` =(((T₆ - T₇) + (T₈ - T₉)) -((T₂ - T₁) + (T₄ - T₃)))/((T₆ - T₅) + (T₈ - T₇))

(((1400 - 1086.08) + (1400 -1086.08 ))-((446.0625 - 300)+(194.881 - 300)))/((1400 -958.0765 ) + (1400 -1086.08 )) = 0.7765

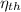`\eta _(th)` = 77.65%

b. Back work ratio, bwr =
`bwr = (w_(c,in))/(w_(t,out))`

((446.0625 - 300)+(194.881 - 300))/((1400 - 1086.08) + (1400 -1086.08 ))

40.9435/627.84 = 6.5%

c.
`w_(net, out) = c_p[(T_6 -T_7) + (T_8 - T_9)] - [(T_2 - T_1) + (T_4 -T_3)]`

Power developed is given by the relation;

`\dot m \cdot w_(net, out)`

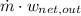
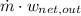`\dot m \cdot w_(net, out)`= 6*1.005*(((1400 - 1086.08) + (1400 -1086.08 ))-((446.0625 - 300)+(194.881 - 300))) = 3538.986 kW

d. Exergy destruction = 6*(1.005*(300-446.0625 ) - 300*1.005*(-0.3966766)

-163.169 kJ