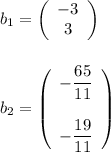Question

If Aequals[Start 2 By 2 Matrix 1st Row 1st Column 1 2nd Column negative 4 2nd Row 1st Column negative 4 2nd Column 5 EndMatrix ] and ABequals[Start 2 By 3 Matrix 1st Row 1st Column negative 10 2nd Column 1 3rd Column 9 2nd Row 1st Column 7 2nd Column negative 15 3rd Column 8 EndMatrix ]​, determine the first and second columns of B. Let Bold b 1 be column 1 of B and Bold b 2 be colum

Answer 1

option c

Explanation:

it is said that a computer repairman makes 25 dollars per hour

this column shows the right amount of money he earns per hour

Answer 2

`b_1=\left(\begin{array}{ccc}-3\\3\end{array}\right),b_2=\left(\begin{array}{ccc}-(65)/(11)\\\\-(19)/(11)\end{array}\right)`

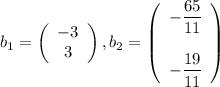
Explanation:

Given matrix A and AB below:

`A=\left(\begin{array}{ccc}1&-4\\-4&5\end{array}\right)\\\\\\ AB=\left(\begin{array}{ccc}-10&1&9\\7&-15&8\end{array}\right)`

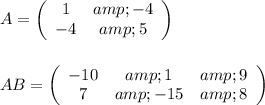
For the product AB to be a 2 X 3 matrix, B must be a 2 X 3 matrix.

Let matrix B be defined as follows

`B=\left[\begin{array}{ccc}a&c&e\\b&d&f\end{array}\right]`

Therefore:

`\left(\begin{array}{ccc}1&-4\\-4&5\end{array}\right)\left(\begin{array}{ccc}a&c&e\\b&d&f\end{array}\right)=\left(\begin{array}{ccc}-10&1&9\\7&-15&8\end{array}\right)`

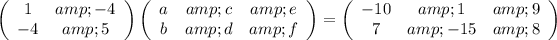
This results in the equations

• a-4b=-10
• -4a+5b=7

• c-4d=1
• -4c+5d=-15

Solving the first two equations simultaneously

a-4b=-10 (a=-10+4b)

-4a+5b=7

Substitution of
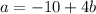`a=-10+4b` into the second equation

`-4(-10+4b)+5b=7\\40-16b+5b=7\\-11b=-33\\b=3`

Recall that
`a=-10+4b`

`a=-10+4(3)=-10+7\\a=-3`

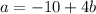
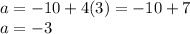
Solving the other two equations

c-4d=1 (c=1+4d)

-4c+5d=-15

Substitution of c=1+4d into the second equation

`-4(1+4d)+5d=-15\\-4-16d+5d=15\\-11d=19\\d=-(19)/(11)\\ Recall: c=1+4d\\c=1+4(-(19)/(11))\\c=-(65)/(11)`

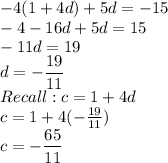
Therefore, we have:

`a=-3, b=3, c=-(65)/(11), d=-(19)/(11)`

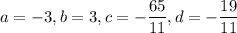
Thus:

`b_1=\left(\begin{array}{ccc}-3\\3\end{array}\right)\\\\\\b_2=\left(\begin{array}{ccc}-(65)/(11)\\\\-(19)/(11)\end{array}\right)`