Answer:
a) 0.2135 = 21.35% probability that overbooking occurs.
b) 0.4625 = 46.25% probability that the flight has empty seats.
Explanation:
For each booked passengers, there are only two possible outcomes. Either they arrive, or they do not. The probability of a passenger arriving is independent of other passengers. So we use the binomial probability distribution to solve this question.
Binomial probability distribution
The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

In which
 is the number of different combinations of x objects from a set of n elements, given by the following formula.
is the number of different combinations of x objects from a set of n elements, given by the following formula.

And p is the probability of X happening.
We are interest in the 19-14 = 5 remaining reservations, each of whom arrive with 52% probability
This means that
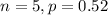
a. Find the probability that overbooking occurs.
There are 17-14 = 3 seats remaining. So overbooking occurs if more than 3 arrive.
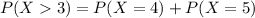


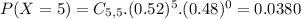
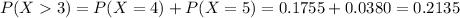
21.35% probability that overbooking occurs.
b. Find the probability that the flight has empty seats.
3 seats remaining, so this is the probability that less than 3 passengers arrive.
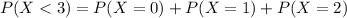
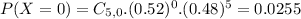

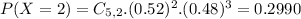
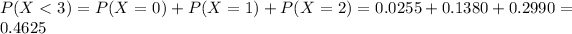
0.4625 = 46.25% probability that the flight has empty seats.