Question

A ductile hot-rolled steel bar has a minimum yield strength in tension and compression of 350 MPa. Using the distortion-energy and maximum-shear-stress theories, determine the factors of safety for the following plane stress states.

a. σx = 94 MPa, and τxy = -75 MPa
b. σx = 110 MPa, σy = 100 MPa
c. σx = 90 MPa, σy = 20 MPa, τxy =−20 MPa

Answer 1

Step-by-step explanation:

From the given question:

Using the distortion energy theory to determine the factors of safety FOS can be expressed by the relation:

`(Syt)/(FOS)= \sqrt{ \sigma x^2+\sigma y^2-\sigma x \sigma y+3 \tau_(xy^2)}`

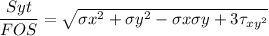
where; syt = strength in tension and compression = 350 MPa

The maximum shear stress theory can be expressed as:

`\tau_(max) = (Syt)/(2FOS)`

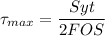
where;

`\tau_(max) =\sqrt{ ((\sigma x-\sigma y)/(2))^2+ \tau _{xy^2`

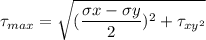
a. Using distortion - energy theory formula:

`(350)/(FOS)= √(94^2+0^2-94*0+3 (-75)^2)}`

`(350)/(FOS)=160.35`

`{FOS}=(350)/(160.35)`

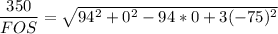
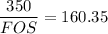
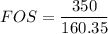
FOS = 2.183

USing the maximum-shear stress theory;

`(350)/(2 FOS) =\sqrt{ ((94-0)/(2))^2+ (-75)^2`

`(350)/(2 FOS) =88.51`

`(350)/( FOS) =2 * 88.51`

`{ FOS} =(350)/(2 * 88.51)`

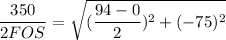
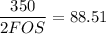
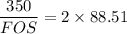
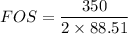
FOS = 1.977

b. σx = 110 MPa, σy = 100 MPa

Using distortion - energy theory formula:

`(350)/(FOS)= √( 110^2+100^2-110*100+3(0)^2)`

`(350)/(FOS)= \sqrt{ 12100+10000-11000`

`(350)/(FOS)=105.3565`

`FOS=(350)/(105.3565)`

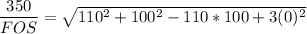
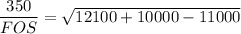
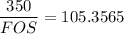
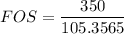
FOS =3.322

USing the maximum-shear stress theory;

`(350)/(2 FOS) =\sqrt{ ((110-100)/(2))^2+ (0)^2`

`(350)/(2 FOS) ={ ((110-100)/(2))^2`

`(350)/(2 FOS) =25`

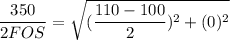
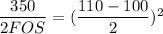
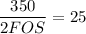
FOS = 350/2×25

FOS = 350/50

FOS = 70

c. σx = 90 MPa, σy = 20 MPa, τxy =−20 MPa

Using distortion- energy theory formula:

`(350)/(FOS)= √( 90^2+20^2-90*20+3(-20)^2)`

`(350)/(FOS)= √( 8100+400-1800+1200)`

`(350)/(FOS)= 88.88`

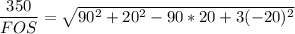
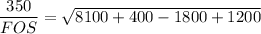
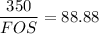
FOS = 350/88.88

FOS = 3.939

USing the maximum-shear stress theory;

`(350)/(2 FOS) =\sqrt{ ((90-20)/(2))^2+ (-20)^2`

`(350)/(2 FOS) =\sqrt{ (35)^2+ (-20)^2`

`(350)/(2 FOS) =\sqrt{ 1225+ 400`

`(350)/(2 FOS) =40.31`

`FOS} =(350)/(2*40.31)`

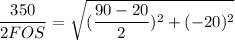
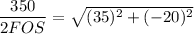
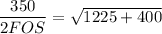
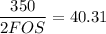
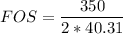
FOS = 4.341