Question

Evaluate the limit, if it exists.
lim (h - > 0) ((-7 + h)^2 - 49) / h

Answer 1

Expand everything in the limit:

`\displaystyle\lim_(h\to0)\frac{(-7+h)^2-49}h=\lim_(h\to0)\frac{(49-14h+h^2)-49}h=\lim_(h\to0)\frac{h^2-14h}h`

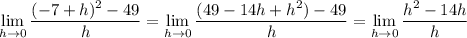
We have
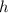`h` approaching 0, and in particular
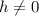`h\\eq0`, so we can cancel a factor in the numerator and denominator:

`\displaystyle\lim_(h\to0)\frac{h^2-14h}h=\lim_(h\to0)(h-14)=\boxed{-14}`

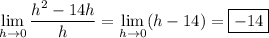
Alternatively, if you already know about derivatives, consider the function
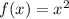`f(x)=x^2`, whose derivative is
`f'(x)=2x`.

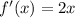Using the limit definition, we have

`f'(x)=\displaystyle\lim_(h\to0)\frac{f(x+h)-f(x)}h=\lim_(h\to0)\frac{(x+h)^2-x^2}h`

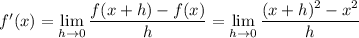
which is exactly the original limit with
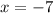`x=-7`. The derivative is
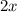`2x`, so the value of the limit is, again, -14.