Expand everything in the limit:
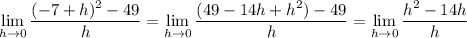
We have
 approaching 0, and in particular
approaching 0, and in particular
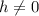 , so we can cancel a factor in the numerator and denominator:
, so we can cancel a factor in the numerator and denominator:
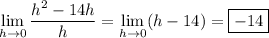
Alternatively, if you already know about derivatives, consider the function
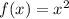 , whose derivative is
, whose derivative is
 .
.
Using the limit definition, we have
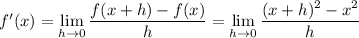
which is exactly the original limit with
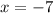 . The derivative is
. The derivative is
 , so the value of the limit is, again, -14.
, so the value of the limit is, again, -14.