Question

an ideal gas is at a pressure 1.00 x 10^5 N/m^2 and occupies a volume 11.00 m^3. If the gass is compressed to a volume of 1.00 m^3 while the temperature remains constant, what will be the new pressure in the gas.

Answer 1

`P_2=1.1x10^6Pa`

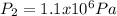
Step-by-step explanation:

Hello.

In this case, we can solve this problem by applying the Boyle's law which allows us to understand the pressure-volume behavior as a directly proportional relationship:

`P_1V_1=P_2V_2`

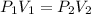
In such away, knowing the both the initial pressure and volume and the final volume, we can compute the final pressure as shown below:

`P_2=(P_1V_1)/(V_2)`

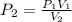
Consider that the given initial pressure is also equal to Pa:

`P_2=(1.00x10^5Pa*11.00m^3)/(1.00m^3)\\ \\P_2=1.1x10^6Pa`

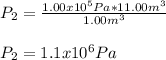
Which stands for a pressure increase when volume decreases.

Regards.