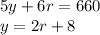Answer:
Correct answer is:
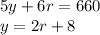
Explanation:
Given that Number of bracelets with yellow beads is represented by

Each bracelet with yellow beads is sold for $5.
Total money raised by bracelets with yellow beads = Number of bracelets sold
 Money raised by sale of one such bracelet =
Money raised by sale of one such bracelet =
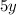
Also Given that Number of bracelets with Orange beads is represented by

Each bracelet with orange beads is sold for $6.
Total money raised by bracelets with orange beads = Number of bracelets sold
 Money raised by sale of one such bracelet =
Money raised by sale of one such bracelet =
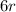
Given that total money raised by sale of both type of bracelets is $660.
so, the first equation becomes:
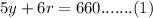
It is also given that "The number of bracelets with yellow beads that Sierra sold is 8 more than twice the number of bracelets with orange beads"

So, by equation (1) and (2), the system of equations is: