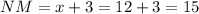Question

Please Help me Find NM using Secant

Answer 1

NM = 15

Explanation:

There is a property of secants and tangents to a circle where:

The square of the tangent length is equal the length of the external segment of the secant times the whole secant length.

Therefore, in our question, we have that:

`NM^2 = ML * MK`

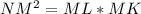
The values of NM, ML and MK are:

`NM = x + 3`

`ML = x - 3`

`MK = ML + LK = x - 3 + 16 = x + 13`

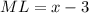
So we have:

`(x+3)^2 = (x - 3)(x + 13)`

`x^2 + 6x + 9 = x^2 + 10x - 39`

`6x + 9 = 10x - 39`

`4x = 48`

`x = 12`

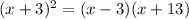
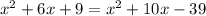
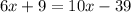
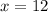
So the length of NM is:

`NM = x + 3 = 12 + 3 = 15`