Answer:
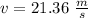
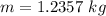
Step-by-step explanation:
Recall the formula for linear momentum (p):
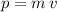 which in our case equals 26.4 kg m/s
which in our case equals 26.4 kg m/s
and notice that the kinetic energy can be written in terms of the linear momentum (p) as shown below:

Then, we can solve for the mass (m) given the information we have on the kinetic energy and momentum of the particle:

Now by knowing the particle's mass, we use the momentum formula to find its speed:
