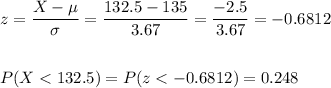Answer:
a) We expect to have 135 people to have had chickenpox in their childhood.
b) No, I would not be surprised, as the probability is not low.
z = -0.6812
c) P(X≤132)=0.248
Explanation:
a) This is a binomial random variable, with n=150 and p=0.9, so we can calculate the expected value as:

b) To answer this we can calculate the probability that 132 people or fewer have had chickenpox in their childhood.
This binomial random variable can be approximated by a normal distribution, with the following parameters:
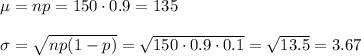
To calculate the probability that 132 people or fewer have had chickenpox in their childhood we compute the z-score for X=132.5 (as we apply the continuity factor) and calculate the probability using the standard normal distribution: