Answer:
B
Explanation:
(Looking at the lines in the graph, the second equation is missing a minus sign, and should be
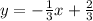 )
)
To find the intersection point of the pair of linear equations, we just need to equate both values of y.
The equations are:
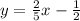
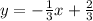
Making the y from one equation equal the y of the other equation, we have:
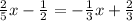
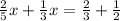
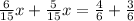
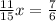
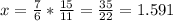
Then the y-coordinate of the point is found using this x-value in any of the two equations:
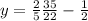
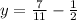
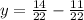
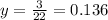
So the coordinate of the crossing point is (1.591, 0.136)
The point that is in this coordinate in the graph is point B.