Answer:
Correct option: B. 90%
Step-by-step explanation:
The confidence interval is given by:
![CI = [\bar{x} - z\sigma_{\bar{x}} , \bar{x}+z\sigma_{\bar{x}} ]](https://img.qammunity.org/2021/formulas/engineering/college/ugc5ibfx7j7t194vfts240rpg6q3uu5717.png)
If
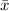 is 190, we can find the value of
is 190, we can find the value of
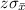 :
:
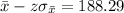
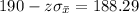
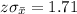
Now we need to find the value of
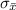 :
:
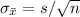
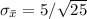
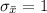
So the value of z is 1.71.
Looking at the z-table, the z value that gives a z-score of 1.71 is 0.0436
This value will occur in both sides of the normal curve, so the confidence level is:
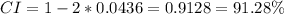
The nearest CI in the options is 90%, so the correct option is B.