Twenty-five wooden beams were ordered or a construction project. The sample mean and he sample standard deviation were measured xbar = 190cm, s = 5cm. Calculated confidence inte…

Question

asked May 26, 2021 141k views

1 Answer

Mitch Satchwell · Answer 1 · 2021-05-31T17:59:37+0000

Answer:

Correct option: B. 90%

Step-by-step explanation:

The confidence interval is given by:

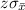$CI = [\bar{x} - z\sigma_{\bar{x}} , \bar{x}+z\sigma_{\bar{x}} ]$

If
$\bar{x}$ is 190, we can find the value of
$z\sigma_{\bar{x}}$ :

$\bar{x} - z\sigma_{\bar{x}} = 188.29$

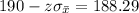
$190 - z\sigma_{\bar{x}} = 188.29$

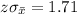
$z\sigma_{\bar{x}} = 1.71$

Now we need to find the value of
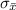$\sigma_{\bar{x}}$ :

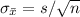
$\sigma_{\bar{x}} = s / √(n)$

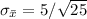
$\sigma_{\bar{x}} = 5/ √(25)$

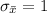
$\sigma_{\bar{x}} = 1$

So the value of z is 1.71.

Looking at the z-table, the z value that gives a z-score of 1.71 is 0.0436

This value will occur in both sides of the normal curve, so the confidence level is:

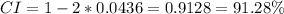
$CI = 1 - 2*0.0436 = 0.9128 = 91.28\%$

The nearest CI in the options is 90%, so the correct option is B.