Question

Assume that a sample is used to estimate a population proportion p. Find the 95% confidence interval for a sample of size 238 with 172 successes. Enter your answer as a tri-linear inequality using decimals (not percents) accurate to three decimal places.

Answer 1

95% confidence interval for a Population proportion

0.6937 ≤ P ≤ 0.7515

Explanation:

Explanation:-

Given sample size 'n' = 238

probability of successes or sample proportion

`p = (x)/(n) = (172)/(238) =0.7226`

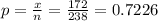
95% confidence interval for a Population proportion is determined by

`(p^(-) - Z_(0.05) \sqrt{(p(1-p))/(n) } , p^(-) + Z_(0.05) \sqrt{(p(1-p))/(n) })`

`(0.7226 - 1.96\sqrt{(0.7226(1-0.7226))/(238) } , 0.7226+ 1.96\sqrt{(0.7226(1-0.7226))/(238) })`

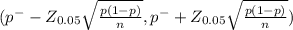
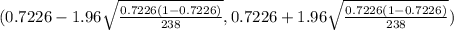
(0.7226 - 0.0289 , 0.7226 + 0.0289)

(0.6937 , 0.7515)

Conclusion:-

95% confidence interval for a Population proportion

0.6937 ≤ P ≤ 0.7515