Question

The point (3, 6) is on the graph of y= 5f(2(x+3))-4 . Find the original point on the graph of y=f(x).

Answer 1

(12, 2) is the original point on the graph of
`y=f(x)`.

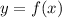Explanation:

Given:

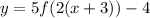`y= 5f(2(x+3))-4` has a point (3, 6) on its graph.

To find:

Original point on graph
`y=f(x)` = ?.

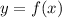Solution:

We are given that The point (3, 6) is on the graph of
`y= 5f(2(x+3))-4`

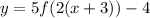
If we put x = 3 and y = 6 in
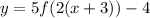`y= 5f(2(x+3))-4`, it will satisfy the equation.

Let us the put the values and observe:

`6= 5f(2(3+3))-4\\\Rightarrow 6= 5f(2(6))-4\\\Rightarrow 6= 5f(12)-4\\\Rightarrow 6+4=5f(12)\\\Rightarrow 5f(12)= 6+4\\\Rightarrow 5f(12)= 10\\\Rightarrow f(12)= (10)/(5)\\\Rightarrow f(12)= 2\\OR\\\Rightarrow 2=f(12)`

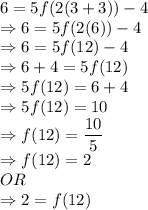
Now, let us compare the above with the following:

`y=f(x)`

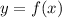
we get y = 2 and x = 12

So, the original point on graph of
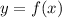`y=f(x)` is (12, 2).