Question

Identify the domain of a radical function with an odd index: A) 0 < x < ∞ B) 0 ≤ x < ∞ C) –∞ < x ≤ 0 D) –∞ < x < ∞

Answer 1

(D)
`-\infty<x< \infty`

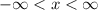
Explanation:

These two basic rules apply when determining the domain of radical functions.

• When the index of the radical function is even, the radicand must be greater than or equal to zero.
• When the index of the radical function is odd, the radicand can be any real number.

For simplicity, the domain of the radical function is the number under the root symbol.

Take for example, the number 2 is even and 3 is odd.

`4^(1/2)=√(4)=2 \\(-4)^(1/2)=√(-4)$ is not a real number`

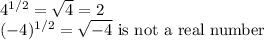
Thus, for even index, the domain must be greater than or equal to zero.

However:

`8^(1/3)=\sqrt[3]{8} =2 \\(-8)^(1/3)=\sqrt[3]{-8}=-2`

Thus, for an odd index, the domain can be any real number from
`-\infty$ to \infty`.

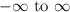The correct option therefore is D.