Answer:
Explanation:
We khow that the equation of a circle is written this way :
(x-a)²+(y-b)²=r² where (x,y) are the coordinates of the cercle's points and (a,b) the coordinates of the cercle's center and r the radius .
Our task is to khow the values of a and b :
- We khow that the center is lying on the line 3x+2y=16⇒ 2y=-3x+16⇒ y=
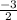 x+8
x+8 - We khow that the points P and Q are two points in the cercle
- Let Ω be the center of this cercle
- we can notice that : PΩ AND QΩ are both equal to the radius ⇒ PΩ=QΩ= r
- So let's write the expression of this distance using vectors KHOWING THAT Ω(a,b)
- Vector PΩ(a-4,b-6) and Vector QΩ(a-8,b-2)
- PΩ=
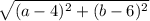 and QΩ=
and QΩ=
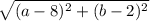
- Let's substitute a by x and b by y
- PΩ=QΩ we substitute each distance by its expression
- After simplyfying the expressions we get finally : -12+8x-8y=0
- now we have -12x +8x-8y=0 and the line equation 3x+2y-16=0
- these are simultanious equations so after solving them we get x=3.8 wich is approximatively 4 and y=2
- we substitute a by 4 and y by 2 in PΩ to get the radius
- we get r =
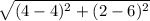 = 4
= 4 - so r²= 16
- then the equation is : (x-4)²+(y-2)²=16