Question

Hi :) how to do question 7 ?

Answer 1

Explanation:

We khow that the equation of a circle is written this way :

(x-a)²+(y-b)²=r² where (x,y) are the coordinates of the cercle's points and (a,b) the coordinates of the cercle's center and r the radius .

Our task is to khow the values of a and b :

• We khow that the center is lying on the line 3x+2y=16⇒ 2y=-3x+16⇒ y=
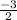  `(-3)/(2)`x+8
• We khow that the points P and Q are two points in the cercle
• Let Ω be the center of this cercle
• we can notice that : PΩ AND QΩ are both equal to the radius ⇒ PΩ=QΩ= r
• So let's write the expression of this distance using vectors KHOWING THAT Ω(a,b)
• Vector PΩ(a-4,b-6) and Vector QΩ(a-8,b-2)
• PΩ=
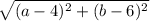  `\sqrt{(a-4)^(2)+(b-6)^(2) }` and QΩ=
  `\sqrt{(a-8)^(2)+(b-2)^(2) }`
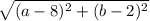
• Let's substitute a by x and b by y
• PΩ=QΩ we substitute each distance by its expression
• After simplyfying the expressions we get finally : -12+8x-8y=0
• now we have -12x +8x-8y=0 and the line equation 3x+2y-16=0
• these are simultanious equations so after solving them we get x=3.8 wich is approximatively 4 and y=2
• we substitute a by 4 and y by 2 in PΩ to get the radius
• we get r =
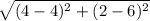  `\sqrt{(4-4)^(2)+(2-6)^(2) }` = 4
• so r²= 16
• then the equation is : (x-4)²+(y-2)²=16