Answer:

And for this case we are analyzing the value os 33.44 and we can use the z score formula given by:
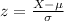
And replacing we got:
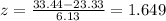
We know that the proportion of area beyond the Z score associated with this age is .05 so then the percentile would be: 95
Explanation:
For this case we have the following parameters:

And for this case we are analyzing the value os 33.44 and we can use the z score formula given by:
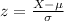
And replacing we got:
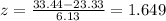
We know that the proportion of area beyond the Z score associated with this age is .05 so then the percentile would be: 95