Answer:
The original length of the edges are equal to 2 cm.
Explanation:
The volume of a cube is given by the following expression:
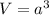
Where "a" is the length of each edge of the cube. Assuming that the original cube had a length of "x", then its volume would be:
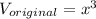
Since the edges of the cube got scaled by a factor of 2, then the new edges are "2*x" and the volume is:
![V_(new) = (2*x)^3\\V_(new) = 8*x^3\\64 = 8*x^3\\x^3 = (64)/(8)\\x^3 = 8\\x = \sqrt[3]{8} = 2](https://img.qammunity.org/2021/formulas/mathematics/high-school/ss40e6hrjmqb04vb1xrpc6g74of1r48w08.png)
The original length of the edges are equal to 2 cm.