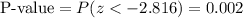Answer:
P-value = 0.002
Explanation:
The claim is that for a smartphone carrier's data speeds at airports, the mean is μ = 10.00 Mbps. This is the null hypothesis that is tested.
Then, the alternative hypothesis will represent the claim that the mean data speed is less than 10.00 Mbps.
We can write this as:

We have a sample size n=32. As the test statistic is z, and not t, we don't need to calculate the degrees of freedom.
The test statistic is z=-2.816. This test is a left-tailed test, so the P-value for this test is calculated as: