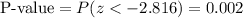Question

Use technology to find the​ P-value for the hypothesis test described below.

The claim is that for a smartphone​ carrier's data speeds at​ airports, the mean is μ = 10.00Mbps. The sample size is n = 32 and the test statistic is z = - 2.816.
What is the p-value?
​(Round to three decimal places as​ needed.)

Answer 1

P-value = 0.002

Explanation:

The claim is that for a smartphone​ carrier's data speeds at​ airports, the mean is μ = 10.00 Mbps. This is the null hypothesis that is tested.

Then, the alternative hypothesis will represent the claim that the mean data speed is less than 10.00 Mbps.

We can write this as:

`H_0: \mu=10\\\\H_a:\mu< 10`

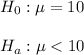
We have a sample size n=32. As the test statistic is z, and not t, we don't need to calculate the degrees of freedom.

The test statistic is z=-2.816. This test is a left-tailed test, so the P-value for this test is calculated as:

`\text{P-value}=P(z<-2.816)=0.002`