Question

Two parallel plates, each of area 7.37 cm2, are separated by 6.00 mm. The space between the plates is filled with air. A voltage of 7.55 V is applied between the plates. Calculate the magnitude of the electric field between the plates. Tries 0/20 Calculate the amount of the electric charge stored on each plate. Tries 0/20 Now distilled water is placed between the plates and the capacitor is charged up again to the same voltage as before. Calculate the magnitude of charge stored on each plate in this case. (Use κ = 80.0 for the dielectric constant of water.)

Answer 1

- E = 1.25*10^3 N/C

- Q = 1.08*10^-12 C

- Q = 8.69*10^-11 C

Step-by-step explanation:

- In order to calculate the magnitude of the electric field between the plates, you use the following formula:

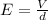`E=(V)/(d)` (1)

V: potential difference between the plates = 7.55V

d: distance between the plates = 6.00mm = 6.00*10^-3m

You replace the values of the parameters n the equation (1):

`E=(7.55V)/(6.00*10^(-3)m)=1.25*10^3(N)/(C)`

The magnitude of the electric field between the plates is 1.25*10^3N/C

- The charge on each plate is given by the following formula:

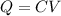`Q=CV` (2)

C: capacitance of the capacitor

The capacitance of a parallel plate capacitor is:

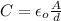`C=\epsilon_o (A)/(d)` (3)

You replace the previous formula into the equation (2) and solve for Q:

`Q=(\epsilon_o k(A)/(d))(V)=(8.85*10^(-12)C^2/Nm^2)(7.37*10^(-4)m^2)/(6.00*10^(-3)m)\\\\Q=1.08*10^(-12)C`

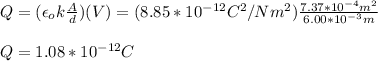
The charge on each plate is 1.08*10^-12C = 1.08pC

- If water is placed in between the plates, the dielectric permittivity is changes by a factor of k = 80.0.

The capacitance of a parallel plate capacitor with a substance with a constant dielectric k, is given by:

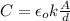`C=\epsilon_o k(A)/(d)` (4)

You replace the previous formula in the equation (2) and replace the values of all parameters:

`Q=(\epsilon_o k(A)/(d))(V)=(8.85*10^(-12)C^2/Nm^2)(80.0)(7.37*10^(-4)m^2)/(6.00*10^(-3)m)\\\\Q=8.69*10^(-11)C`

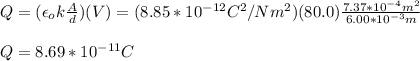
The charges on each plate is 8.69*10^-11 C