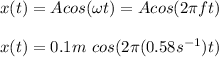Question

g A 1.5-kg mass attached to spring with a force constant of 20.0 N/m oscillates on a horizontal, frictionless track. At t = 0, the mass is released from rest at x = 10.0 cm. ( That is, the spring is stretched by 10.0 cm.) (a) Determine the frequency of the oscillations. (b) Determine the maximum speed of the mass. Where dos the maximum speed occur? (c) Determine the maximum acceleration of the mass. Where does the maximum acceleration occur? (d) Determine the total energy of teh oscillating system. (e) Express the displacement as a function of time.

Answer 1

(a) f = 0.58Hz

(b) vmax = 0.364m/s

(c) amax = 1.32m/s^2

(d) E = 0.1J

(e) x(t)=0.1m*cos(2π(0.58s^{-1})t)

Step-by-step explanation:

(a) The frequency of the oscillation, in a spring-mass system, is calculated by using the following formula:

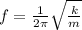`f=(1)/(2\pi)\sqrt{(k)/(m)}` (1)

k: spring constant = 20.0N/m

m: mass = 1.5kg

you replace the values of m and k for getting f:

`f=(1)/(2\pi)\sqrt{(20.0N/m)/(1.5kg)}=0.58s^(-1)=0.58Hz`

The frequency of the oscillation is 0.58Hz

(b) The maximum speed is given by the following relation:

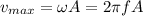`v_(max)=\omega A=2\pi f A` (2)

A: amplitude of the oscillations = 10.0cm = 0.10m

`v_(max)=2\pi (0.58s^(-1))(0.10m)=0.364(m)/(s)`

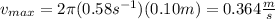
The maximum speed of the mass is 0.364 m/s.

The maximum speed occurs when the mass passes trough the equilibrium point of the oscillation.

(c) The maximum acceleration is given by the following formula:

`a_(max)=\omega^2A=(2\pi f)^2 A`

`a_(max)=(2\pi (0.58s^(-1)))(0.10m)=1.32(m)/(s^2)`

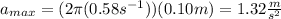
The maximum acceleration is 1.32 m/s^2

The maximum acceleration occurs where the elastic force is a maximum, that is, where the mass is at the maximum distance from the equilibrium point, that is, the acceleration.

(d) The total energy of the system is calculated with the maximum potential elastic energy:

`E=(1)/(2)kA^2=(1)/(2)(20.0N/m)(0.10m)^2=0.1J`

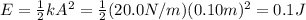
The total energy is 0.1J

(e) The displacement as a function of time is:

`x(t)=Acos(\omega t)=Acos(2\pi ft)\\\\x(t)=0.1m\ cos(2\pi(0.58s^(-1))t)`