Question

The electric field at the surface of a charged, solid, copper sphere with radius 0.220 mm is 4200 N/CN/C, directed toward the center of the sphere. What is the potential at the center of the sphere, if we take the potential to be zero infinitely far from the sphere?

Answer 1

The potential at the center of the sphere is -924 V

Step-by-step explanation:

Given;

radius of the sphere, R = 0.22 m

electric field at the surface of the sphere, E = 4200 N/C

Since the electric field is directed towards the center of the sphere, the charge is negative.

The Potential is the same at every point in the sphere, and it is given as;

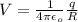`V = (1)/(4 \pi \epsilon_o) (q)/(R)` -------equation (1)

The electric field on the sphere is also given as;

`E = (1)/(4 \pi \epsilon _o) (|q|)/(R^2)`

`|q |= 4 \pi \epsilon _o} R^2E`

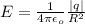
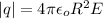
Substitute in the value of q in equation (1)

`V = (1)/(4 \pi \epsilon_o) (-(4 \pi \epsilon _o R^2E))/(R) \ \ \ \ q \ is \ negative\ because \ E \ is\ directed \ toward \ the \ center\\\\V = -RE\\\\V = -(0.22* 4200)\\\\V = -924 \ V`

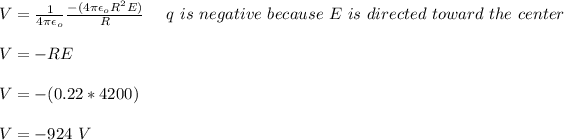
Therefore, the potential at the center of the sphere is -924 V