Question

given the following quantities of reactants and the balance equations; assuming an 85.0% yield, determine how many grams of potassium aluminum sulphate dodecahydrate can be produced.

Answer 1

`m_(KAl(SO_4)_2\dot \ 12H_2O)^(actual)=32.23gKAl(SO_4)_2\dot \ 12H_2O`

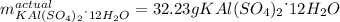
Step-by-step explanation:

Hello,

In this case, we balance the given equations as shown below:

`Al(s)+KOH(aq)+3H_2O(l)\rightarrow KAl(OH)_4(aq)+(3)/(2) H_2(g)\\\\KAl(OH)_4(aq)+2H_2SO_4(aq)\rightarrow KAl(SO_4)_2(aq)+4H_2O(l)\\\\KAl(SO_4)_2(aq)+12H_2O\rightarrow KAl(SO_4)_2\dot\ 12H_2O(aq)`

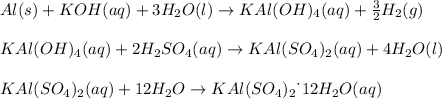
Now, with 3.00 grams of aluminium, 50.00 mL of water and 10.00 mL of 8.00M potassium hydroxide, the first step is to identify the limiting reactant by firstly computing the moles of all of them:

`n_(Al)=3.00 gAl*(1molAl)/(27gAl)=0.111molAl\\ \\n_(KOH)=0.010L*8.00mol/L=0.08molKOH\\\\n_(H_2O)=50.00mL*(1g)/(1mL) *(1mol)/(18g)=2.78molH_2O`

Thus, we can notice that 0.111 mol of aluminium will consume 0.11. moles of potassium hydroxide and 2.78 moles of water will consume 0.927 moles of potassium hydroxide, for that reason, we can infer that since there are only 0.08 moles of potassium hydroxide, it is the limiting reactant, therefore, we compute the yielded moles of potassium aluminium hydroxide in the first reaction:

`n_(KAl(OH)_4)=0.08molKOH*(1molKAl(OH)_4)/(1molKOH) =0.08molKAl(OH)_4`

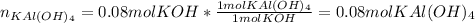
Next, we compute the yielded moles of potassium aluminium sulfate in the second reaction assuming sulfuric acid is in excess:

`n_(KAl(SO_4)_2)=0.08molKAl(OH)_4*(1molKAl(SO_4)_2)/(1molKAl(OH)_4)=0.08molKAl(SO_4)_2`

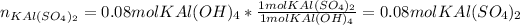
Finally, in the third reaction, we compute the yielded grams of potassium aluminum sulphate dodecahydrate by using its molar mass and its mole ratio with potassium aluminium sulfate:

`m_(KAl(SO_4)_2\dot \ 12H_2O)=0.08molKAl(SO_4)_2*(1molKAl(SO_4)_2\dot \ 12H_2O)/(1molKAl(SO_4)_2) *(474.00gKAl(SO_4)_2\dot \ 12H_2O)/(1molKAl(SO_4)_2\dot \ 12H_2O) \\\\m_(KAl(SO_4)_2\dot \ 12H_2O)=37.92gKAl(SO_4)_2\dot \ 12H_2O`

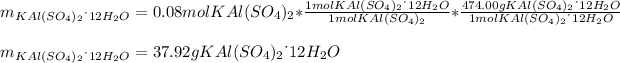
Which is the theoretical yield, thus, by using the percent yield the actual yielded mass turns out:

`m_(KAl(SO_4)_2\dot \ 12H_2O)^(actual)=0.85*37.92gKAl(SO_4)_2\dot \ 12H_2O\\\\m_(KAl(SO_4)_2\dot \ 12H_2O)^(actual)=32.23gKAl(SO_4)_2\dot \ 12H_2O`

Best regards.