Question

In the figure shown two lines intersect at a right angle and two semicircles are drawn so that each semicircle has its diameter on one line and is tangent to the other line. The larger semicircle has radius of 1. The smaller semicircle intersects the larger one, dividing the larger semicircle arc into the ratio 1:5. What is the radius of the smaller semicircle? Express your answer in simplest radical form.

Answer 1

2-√3

Explanation:

In the attached, we have labeled some points so they are easier to talk about.

We are given that arc AG : arc GC = 1 : 5, so the measure of arc AG is 1/6 of the total measure of arc AC. That is, AG = 180°/6 = 30°.

Inscribed angle ACG is half that measure, so is 15°. Triangle BEA is similar to and half the size of triangle CDA, so angle ABE is also 15°. Radius AB is 1, so side AE is tan(15°).

We can use the half-angle formula for tangent to find the measure of AE.

`\tan{15^(\circ)}=\frac{1-\cos{30^(\circ)}}{\sin{30^(\circ)}}=(1-(√(3))/(2))/((1)/(2))=2-√(3)`

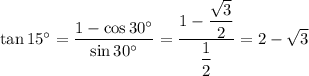
The radius of the smaller circle is 2-√3.