Answer:
2-√3
Explanation:
In the attached, we have labeled some points so they are easier to talk about.
We are given that arc AG : arc GC = 1 : 5, so the measure of arc AG is 1/6 of the total measure of arc AC. That is, AG = 180°/6 = 30°.
Inscribed angle ACG is half that measure, so is 15°. Triangle BEA is similar to and half the size of triangle CDA, so angle ABE is also 15°. Radius AB is 1, so side AE is tan(15°).
We can use the half-angle formula for tangent to find the measure of AE.
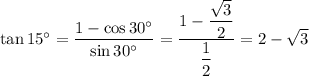
The radius of the smaller circle is 2-√3.