Question

Consider a steel tape measure with cross-sectional area, A = 0.0625 inches squared, and length L = 3, 600 inches at room temperature. How much error will occur if this tape measure is used on a hot day? Assume it is 130F and the coefficient of thermal expansion is α = 5× 10 −6 1/F. Does the error depend on the distance being measured?

Answer 1

e = -0.00031 ( the -ve sign is due to the increase in length)

The error depends on the distance measured

Step-by-step explanation:

Cross Sectional Area of the tape, A = 0.0625 in²

Length of the steel tape, L = 3600 in

Normal room temperature, T₁ = 68°F

Temperature of the hot day, T₂ = 130°F

ΔT = T₂ - T₁ = 130 - 68

ΔT = 62°F

Coefficient of Linear expansion
`\alpha = 5 * 10^(-6) F^(-1)`

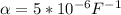
The coefficient of linear expansion is given by the formula:

`\alpha = (\triangle L)/(L* \triangle T) \\\triangle L = \alpha L \triangle T\\\triangle L = 5* 10^(-6) * 3.6* 10^3 * 62\\\triangle L = 1.11 6 in`

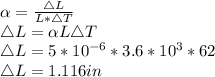
Since the length is increased, the error will be given by the formula:

`e = (-\triangle L)/(L) \\\\e = (-1.116)/(3600)`

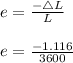
e = -0.00031 ( the -ve sign is due to the increase in length)

Since the error is a function of length and change in length, it depends on the distance measured