Question

PLEASEEE HELPP!!! BRINLIEST TO FIRST ANSWER!!

The dance team has 9 dancers to perform different roles in each performance. The probability that the team selects the same order as last performance is 1 divided by 362880 . -Explain where each the numerator and denominator come from. -What is the probability that the team puts the top hip hop dancer in the third position and top break dancer in the first position? Assume these are not the same people. -Create a question, related to the dancers, where you use the indirect method, n(A’), to solve.

Answer 1

The probability that the team puts the top hip hop dancer in the third position and top break dancer in the first position is 1/72.

Explanation:

It is provided that a dance team has 9 dancers to perform different roles in each performance.

The number of arrangements of the 9 dancers in the different roles is:

Number of order of performance = 9!

= 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1

= 362880

If the team selects the same order as last performance, then the possible number of arrangements is, 1.

The probability that the team selects the same order as last performance is:

`=(1)/(362880)`

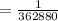
Now it is provided that the team puts the top hip hop dancer in the third position and top break dancer in the first position.

So of the 9 positions the 1st and 3rd are occupied.

There are a remaining 7 positions to be filled by 7 dancers.

That can happen in 7! = 7 × 6 × 5 × 4 × 3 × 2 × 1 = 5040 ways.

Compute the probability that the team puts the top hip hop dancer in the third position and top break dancer in the first position as follows:

`=(5040)/(362880)\\\\=(1)/(72)`

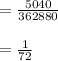
Thus, the probability is 1/72.