Answer:
So if you increase the sample size used to construct a given confidence interval, the confidence interval will be narrower, that is, more precise.
Explanation:
The sample size is important to find the margin of errror of a confidence interval.
The margin of error is given by a formula in the following format:
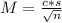
In which c is the critical value(depends on the distribution used, can be T or Z), s is the standard deviation(of the sample or the population) and n is the size of the sample.
As n increases, M decreases, which leads to a lower margin of error.
The lower the margin of error, the more precise the interval is.
So if you increase the sample size used to construct a given confidence interval, the confidence interval will be narrower, that is, more precise.