Question

What will happen (other things being equal) if you increase the sample size used to construct a given confidence interval?

Answer 1

So if you increase the sample size used to construct a given confidence interval, the confidence interval will be narrower, that is, more precise.

Explanation:

The sample size is important to find the margin of errror of a confidence interval.

The margin of error is given by a formula in the following format:

`M = (c*s)/(√(n))`

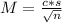
In which c is the critical value(depends on the distribution used, can be T or Z), s is the standard deviation(of the sample or the population) and n is the size of the sample.

As n increases, M decreases, which leads to a lower margin of error.

The lower the margin of error, the more precise the interval is.

So if you increase the sample size used to construct a given confidence interval, the confidence interval will be narrower, that is, more precise.